Beyond unification: A little logic language

In Unification in Elixir, I describe in detail how to implement the unification algorithm. Through two small examples, I also hint at how new layers can be added that make it possible to process more complex logical expressions. In this post, I carry these ideas forward to develop a little logic language (L3) in Elixir. This language captures core aspects of microKanren, a more complete (but still very small) logic programming language. You don't need to have read the microKanren paper to follow along here, but it would be a good idea to skim Unification in Elixir and review the code linked in that post.

Start at the end

Rather than begin with primitive concepts and build up to L3, I'm going to start by demonstrating the interface I'd like to achieve. There are three logic functions that L3 will support: equal, both, and either, each of which takes two arguments. Before discussing how these functions work and what they return, I want to talk about what they mean and how they can be composed to create complex logical expressions.

The simplest of these functions is equal. Like unify, equal takes two terms as arguments and is asserting their equality. For instance, equal(x, 1) asserts that variable x is equal to 1. Another way to say this is that equal(x, 1) returns a goal expressing the idea that x == 1. Depending on the current substitution, this goal may or may not succeed. I'll clearly define what a goal is a bit later.

Logical conjunction is expressed with both. Each of the two arguments to both is a goal. Like equal, both is a function that returns a goal. The expression both(equal(x, y), equal(y, 1)) declares that x == y and y == 1 are jointly true. More complex conjunctions can be constructed through composition:

both(
  equal(x, y),
  both(
    equal(y, z),
    equal(z, 1)
  )
)

Ask yourself, what should the result be if there is no initial knowledge about the variables?

As you might guess, either expresses the logical disjunction of a pair of goals; it also returns a goal. For example, either(equal(x, 1), equal(x, 2)) says that x == 1 or x == 2 may be separately true. Arguments of either and both can be arbitrarily nested compositions of equal, both, and either.

Code written using equal, both, and either is declarative. Even when the implementation details are unknown, the intent is clear when writing something like both(equal(x, y), equal(y, 1)). Declarative code allows one to express intent without procedural distractions. Before addressing the procedural distractions necessities, let's look at more examples.

Familiar examples

Near the end of Unification in Elixir, I discuss two examples, one a logical join of three lists, and the other a series of binary choices. Let's cast these examples in terms of the functions described above. After the functions are fully implemented, I'll return to these examples to get actual results.

Three lists united

Equality of [x, 2, 3] and [1, y, 3] is written as equal([x, 2, 3], [1, y, 3]). With the help of both, multiple equalities may be chained together:

l1 = [x, 2, 3]
l2 = [1, y, 3]
l3 = [1, 2, z]

both(
  equal(l1, l2),
  both(
    equal(l2, l3),
    equal(l1, l3)
  )
)

This doesn't have a with block or :ok tuples or other arcane symbols; it's a concise declaration of intent.

A walk divided

For a person that can step either :left or :right, the first step with direction d1 is written as

either(
  equal(d1, :left),
  equal(d1, :right)
)

For the first two steps:

both(
  either(
    equal(d1, :left),
    equal(d1, :right)
  ),
  either(
    equal(d2, :left),
    equal(d2, :right)
  )
)

For the first three steps:

both(
  either(
    equal(d1, :left),
    equal(d1, :right)
  ),
  both(
    either(
      equal(d2, :left),
      equal(d2, :right)
    ),
    either(
      equal(d3, :left),
      equal(d3, :right)
    )
  )
)

And so on.

This is much less code and is arguably much more readable than what was presented in Unification in Elixir. That's by design! L3 is a declarative domain-specific language, one whose sole purpose is to clearly express and evaluate logical ideas.

Goal setting

We're writing code to solve problems. Declarations of intent are not enough. Somewhere, somehow those declarations need to act on data to produce new data. I said earlier that equal, both, and either return goals when provided with arguments. And both and either take goals as arguments. But what is a goal?

An assertion like equal(x, 1) must be evaluated in the context of what is already known. Recall that a single state of knowledge is represented by a substitution, a mapping between variables and their values. Whatever equal(x, 1) returns, it must be able to act on a substitution. A goal is a function of a substitution. What does this function produce when called?

When given the empty substitution, %{} (nothing is known), the goal generated by equal(x, 1) should return the updated substitution %{x => 1}. Maybe a goal returns a new substitution? Not so fast!

When the disjunction either(equal(x, 1), equal(x, 2)) is given an empty substitution, it should yield [%{x => 1}, %{x => 2}]. A list of substitutions, one that reflects all possible choices, is the most general state of knowledge, at least for our purposes. Even though the goal corresponding to equal(x, 1) doesn't spawn multiple substitutions, it still returns a list to be compatible with either. The same goes for goals generated by both.

A goal is a function that takes a substitution and returns a list of substitutions. To help solidify this idea, here's an elixir type definition:

@type goal :: (substitution -> [substitution])

The list may be empty. This happens when the assertion is in conflict with the substitution supplied to the goal. If we know %{x => 2}, then equal(x, 1) is a false assertion, and the goal must return [].

A little logic language

The interface to L3 has been described, and the abstract notion of a goal has been defined. It's now time to fully implement the specific goals returned by equal, both, and either.

equal(term1, term2)

Recall that unify implements term equality in the context of a substitution. Unsurprisingly, equal is just a lightweight wrapper around unify:

@spec equal(uterm, uterm) :: goal
def equal(term1, term2) do
  fn sub ->
    case unify(sub, term1, term2) do
      {:ok, sub} -> [sub]
      :error -> []
    end
  end
end

The goal repackages the result of unify so that a list is returned. The result of equal(x, 1).(%{}) is [%{x => 1}], as expected, while equal(x, 1).(%{x => 2}) is a conflict and yields [].

both(goal1, goal2)

A conjunction involves a mapping of one goal over the results of another. First, apply goal1 to the input substitution to generate a list of new substitutions. Then, for each of these substitutions, apply goal2. The output of these two steps is a nested list of substitutions. Finally, flatten the nested list to return one list of substitutions that represents the combined result. The Elixir function Enum.flat_map does the job nicely:

@spec both(goal, goal) :: goal
def both(goal1, goal2) do
  fn sub ->
    Enum.flat_map(goal1.(sub), goal2)
  end
end

Here's a diagram that illustrates both:

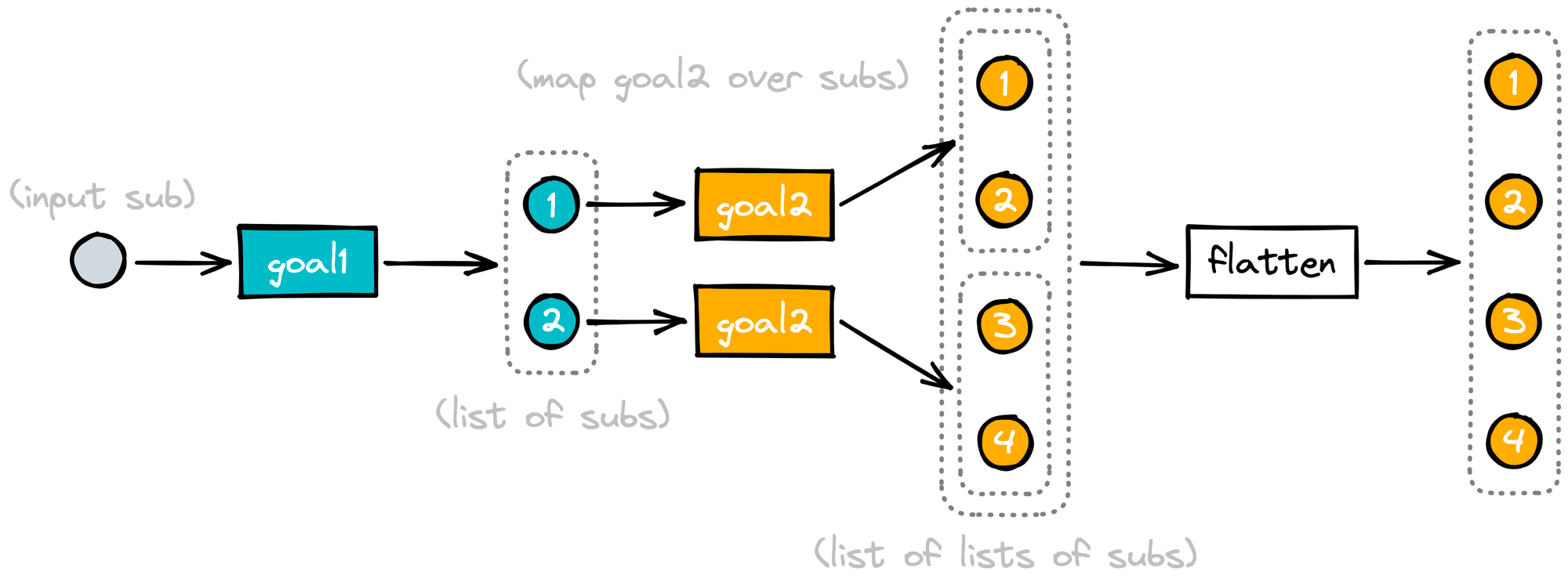
The circles are substitutions, the boxes with solid borders are functions, and the dashed boxes are lists. Colors indicate a goal or substitutions generated by the goal with matching color. Numbers indicate unique substitutions with a given color. In this illustrative example, I assume that each of the goals generates two substitutions.

You might be wondering if the result of both changes when the order of its arguments is swapped. In a certain technical sense, the result does change. But this change is an artifact of using lists to hold substitutions–a computational convenience. If the result is cast to a set (in Elixir, a MapSet) and all variables are fully simplified, you'll see that answer is the same before and after the argument swap. (There is a caveat to this when one or both goals can produce an infinite number of substitutions, but that's outside the scope of this post.)

either(goal1, goal2)

Each goal supplied to either generates a separate list of substitutions. To match the structure of the desired result, these two lists are combined. The simplest way to combine two lists is to concatenate them, as seen here:

@spec either(goal, goal) :: goal
def either(goal1, goal2) do
  fn sub ->
    Enum.concat(goal1.(sub), goal2.(sub))
  end
end

And here's an illustrative diagram for either:

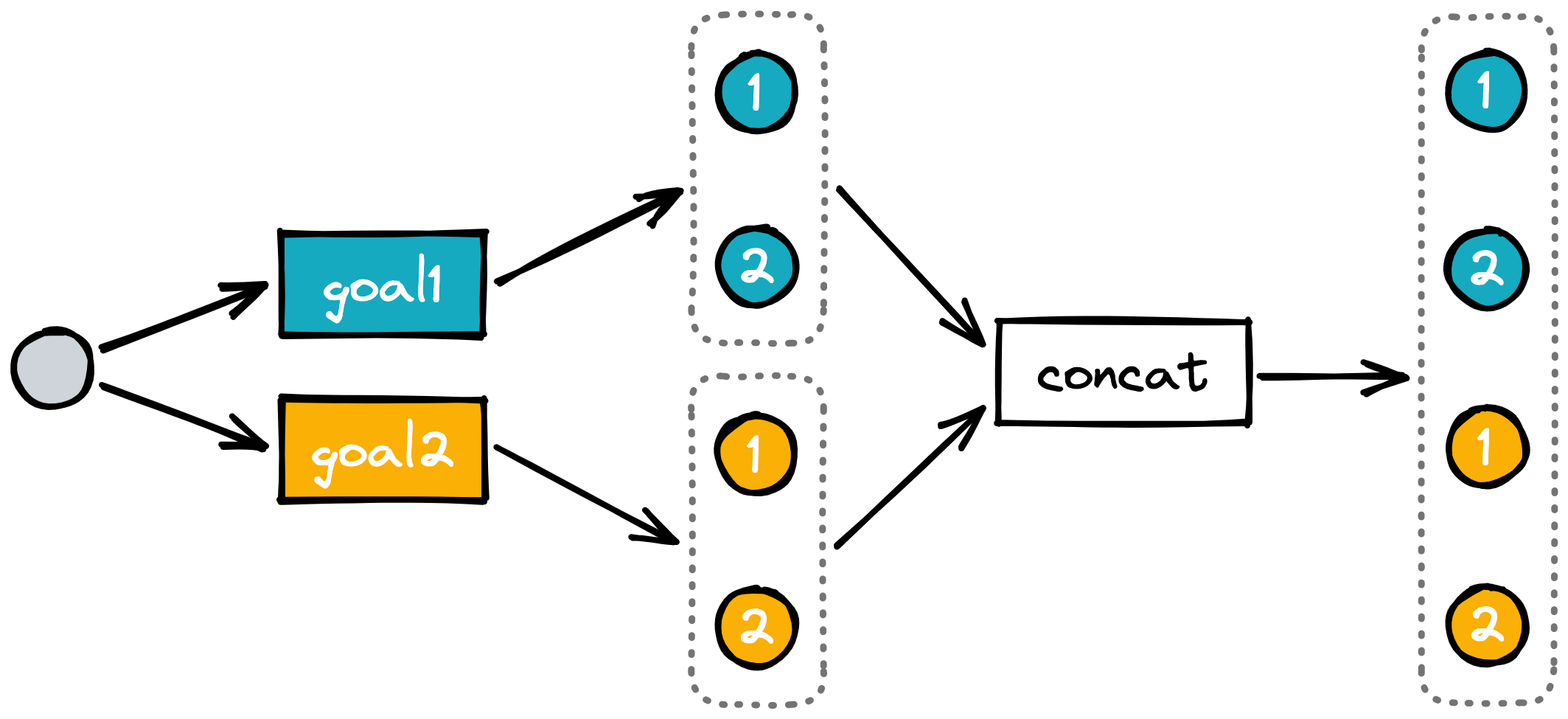
The order of the arguments to either doesn't have a material effect on the results.

A little help

It feels clunky to call goals directly. Here's a helper function that takes a goal and a list of variables, and returns simplified values (via simplify):

@spec present(goal, [variable]) :: [uterm]
def present(goal, vars) do
  %{}
  |> goal.()
  |> Enum.map(&present_sub(&1, vars))
end

defp present_sub(sub, vars) do
  Enum.map(vars, fn v ->
    if Map.has_key?(sub, v) do
      simplify(sub, v)
    else
      v
    end
  end)
end

This function calls the goal with an empty substitution and then applies simplify to the variables for each member of the returned list of substitutions. Putting present to use looks like this:

both(
  either(
  	equal(x, 1), 
    equal(x, y)
   ),
  either(
    equal(y, 2),
    equal(y, 3)
  )
)
|> present([x, y])

# returns

[[1, 2], [1, 3], [2, 2], [3, 3]]

If a variable given to present isn't a substitution key, then the unresolved variable is included in the output:

equal(x, 1) 
|> present([x, y])

# returns

[[1, y]]

Revisited examples

Now that the L3 logic functions are implemented, the examples from earlier can be evaluated. For the joint unification of three lists, calling on an empty substitution yields the expected result:

both(
  equal(l1, l2),
  both(
    equal(l2, l3),
    equal(l1, l3)
  )
)
|> present([x, y, z])

# returns

[[1, 2, 3]]

In the case of the random walk, the possibilities after two steps are

both(
  either(
    equal(d1, :left),
    equal(d1, :right)
  ),
  either(
    equal(d2, :left),
    equal(d2, :right)
  )
)
|> present([d1, d2])

# returns

[
  [:left, :left],
  [:left, :right], 
  [:right, :left], 
  [:right, :right]
]

It's incredibly satisfying to see our hard hard work culminate in such a simple and expressive little language.

The end?

There's so much more we could do with L3, from quality-of-life improvements to deeper applications. I hope to explore some of these ideas in later posts. Until then, if you'd like to play with L3, all the code can be found here:

A little logic language.

Have fun!