Elixir Drop: Pinning in comprehensions

This is a short one. Just a little drop of Elixir--a droplet, even.

One of the things I most appreciate about Elixir is the pervasiveness and consistency of pattern matching. Pattern matching can be used almost everywhere, even when you least expect it.

Recently, I had a little problem involving graphs with weighted edges. The picture below illustrates what I'm talking about.  

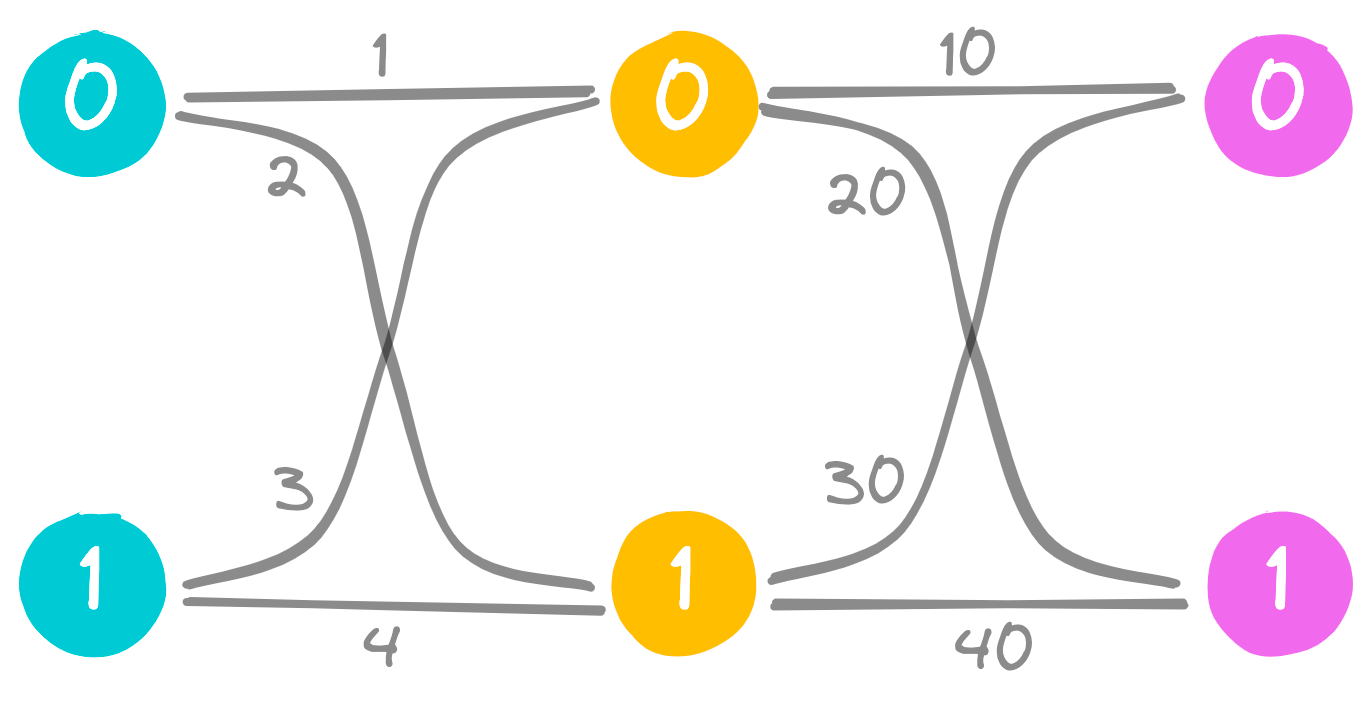
The graph relationships are provided as a pair of maps. One map represents the edges and weights from the cyan (left-most) to the orange (middle) nodes. The second map has the edges and weights connecting the orange to the purple (right-most) nodes.

left_to_middle = %{
  {0, 0} => 1,
  {0, 1} => 2,
  {1, 0} => 3,
  {1, 1} => 4
}

middle_to_right = %{
  {0, 0} => 10,
  {0, 1} => 20,
  {1, 0} => 30,
  {1, 1} => 40
}

Notice that a key in left_to_middle has the form {left_id, middle_id}, while in middle_to_right each key is {middle_id, right_id}.

A connected path from left to right is a pair of edges, one from left to middle, the other from middle to right, where the middle node is common between the two edges. One such path is shown below.

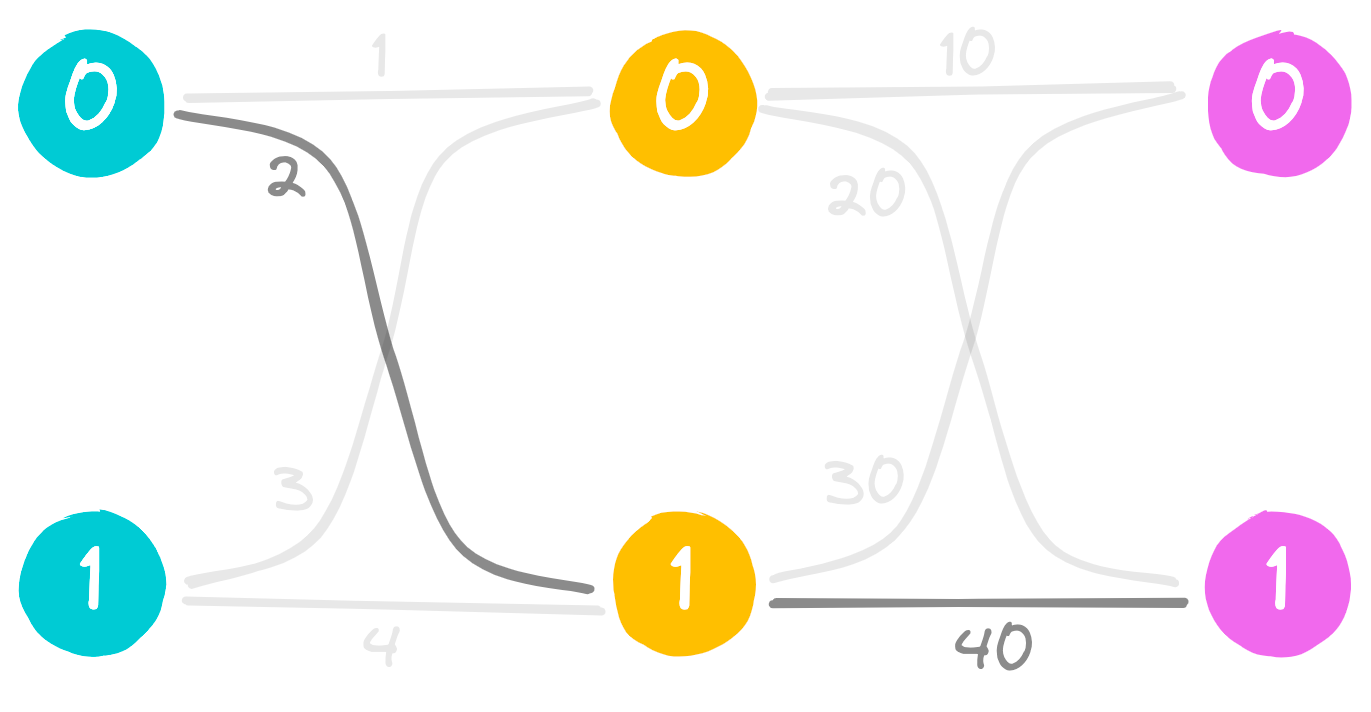
Since the middle node is common for each of the edges, the path can be represented as {left_id, middle_id, right_id}. The path in the figure is {0, 1, 1}. There are 8 connected paths in this graph. For the problem of interest, the weight of a connected path is the sum of the edge weights. The path {0, 1, 1} has weight 2 + 40 = 42.

Our task is to combine the pair of maps above into a single map that shows all connected paths and their respective weights. I'll spare you the tedious discussion of the different ways this can be done in Elixir, and jump right to an answer. Here's a nifty way to do it with a single comprehension:

for {{left, middle}, w_lm} <- left_to_middle,
    {{^middle, right}, w_mr} <- middle_to_right,
    into: %{},
    do: {{left, middle, right}, w_lm + w_mr}

The part that I think is neat is ^middle in the second (inner) generator, which pins the middle node ID to the value in the first (outer) generator. This has the effect of filtering the keys--via pattern matching--in middle_to_right to match the middle node ID in left_to_middle. Feel free to confirm for yourself that this comprehension gives the expected result:

%{
  {0, 0, 0} => 11,
  {0, 0, 1} => 21,
  {0, 1, 0} => 32,
  {0, 1, 1} => 42,
  {1, 0, 0} => 13,
  {1, 0, 1} => 23,
  {1, 1, 0} => 34,
  {1, 1, 1} => 44
}

In case you're wondering, I figured this out just by trying it. I knew that pattern matching works as a filter in comprehensions, but I hadn't come across the use of pinning. I thought, Hm, I wonder if that'll work? And it did!