Elixir Drop: Mergesort

In this Drop, I'll walk through the Elixir implementation of Mergesort, a well-known sorting algorithm and one of the earliest divide-and-conquer algorithms developed for digital computers. This is as much a fun exercise as it is a demonstration of how one common algorithm can be implemented in a functional language.

Many of the Mergesort implementations online assume you're working with arrays, data structures that support constant-time lookup. While Mergesort could be implemented with Erlang's array or Elixir's Map (neither of which have constant-time lookup in general), it might be more instructive (and fun!) to stick with ordinary Elixir lists.

I'll begin by stating the goal: the function sort takes a list of sortable items and returns a new list with the items sorted. It would work like this:

> sort([5, 1, 11, 7])
[1, 5, 7, 11]

Simple enough. How do we get to this result?

Schematically, sort can be defined as:

@spec sort(list()) :: list()
def sort([]), do: []

def sort([item]), do: [item]

def sort([_ | _] = list) do
  # do the sorting
end

In the first two function clauses, the input lists are already sorted, and so the input is passed through as the returned value. The third clause is where the real work get done.

In words, Mergesort can described quite simply:

When sorting a list, first divide the list into a left half and a right half. Then sort the left and right halves. Finally, merge the sorted left and right halves into the final sorted list.

Notice that this description is inherently recursive. The verbal expression of Mergesort can be translated immediately into valid Elixir code:

def sort([_ | _] = list) do
  {left, right} = divide(list)
  
  left_sorted = sort(left)
  right_sorted = sort(right)

  merge_sorted(left_sorted, right_sorted)
end

Now the functions divide and merge_sorted need to be defined.

Dividing a list in Elixir can be accomplished with a suitable application of Enum.reduce, but Elixir already has us covered with Enum.split(enumerable, count). From the docs, split is defined as

Splits the enumerable into two enumerables, leaving count elements in the first one.

Perfect! Here's divide:

@spec divide(list()) :: {list(), list()}
def divide(list) do
  Enum.split(list, ceil(length(list) / 2))
end

The ceil function rounds up, so that ceil(5/2) = 3. A list with length 4 will be divided into two lists of length 2, while a list with 5 elements will be divided into a list with length 3 and a list with length 2. Here it is in action:

> divide([1, 2, 3, 4])
{[1, 2], [3, 4]}

> divide([1, 2, 3, 4, 5])
{[1, 2, 3], [4, 5]}

> divide([1])
{[1], []}

> divide([])
{[], []}

Note that split walks through the list until a stopping condition is satisfied. This means that split is an O(N) operation, where N is the length of the list.

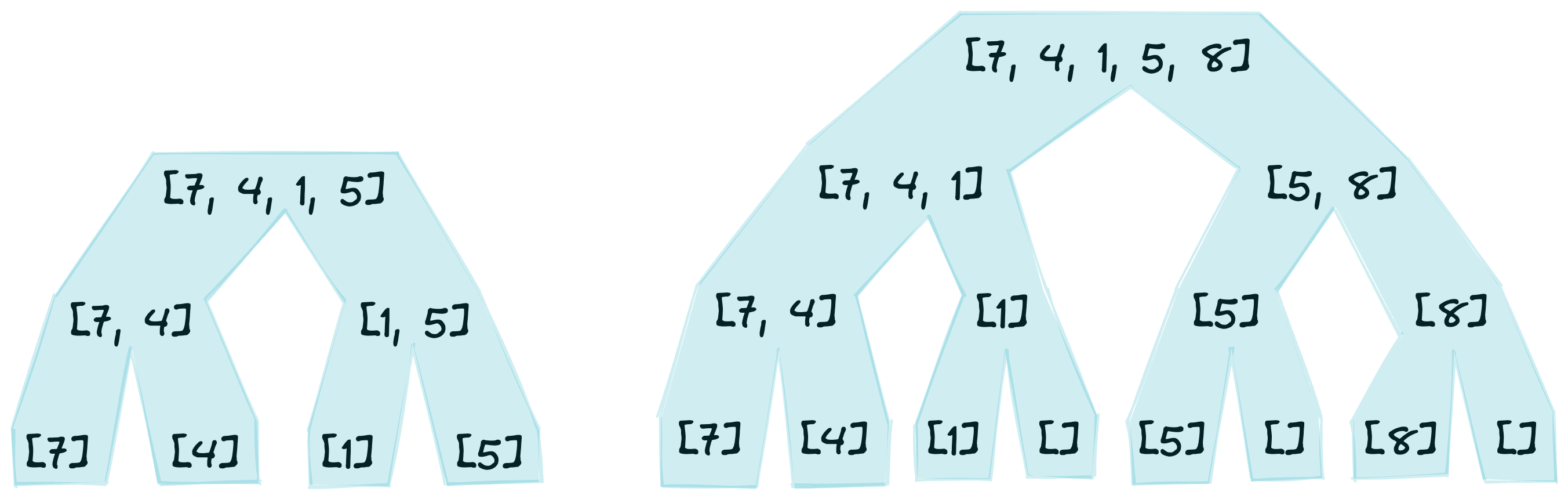
During recursion in the sort function, left and right will eventually be either empty or a list with one element. These are the recursive base cases, and are handled by the first two clauses in the definition of sort. Shown in the figure below are two examples of recursively dividing a list into its smallest pieces.

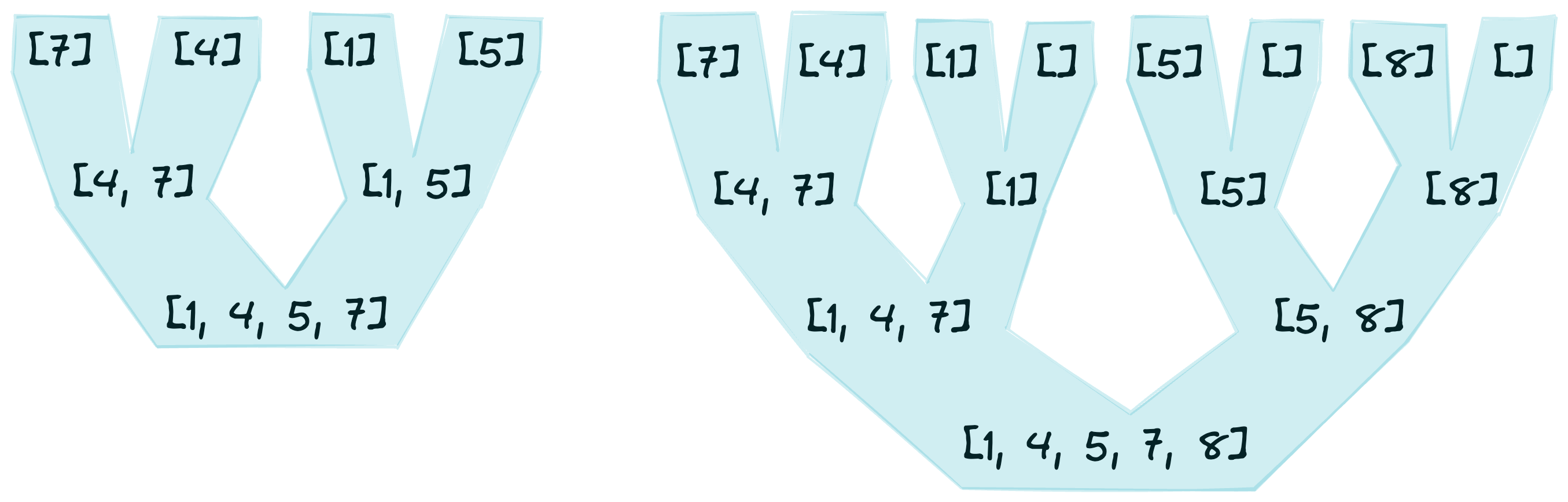
When the base cases cases are reached, the merge process begins. The figure below shows the merger of sorted lists, building from the base cases to the final sorted list.

When merge_sorted is first called, each of its arguments will be either an empty list or a list with one element, both of which are already sorted, by definition.

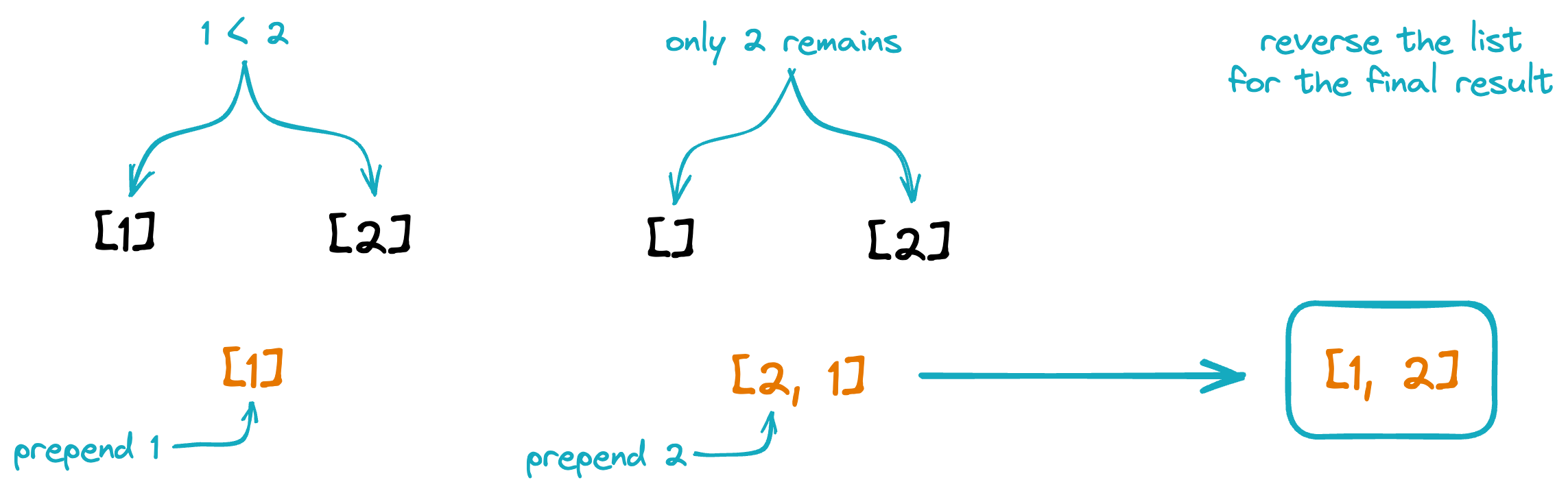
The figure below shows an example of merging two length-1 lists into a sorted list of length 2. At each step of the merger, the heads of the lists are compared, and the smaller value is prepended to the accumulating output list. The output must be reversed to obtain the final result.

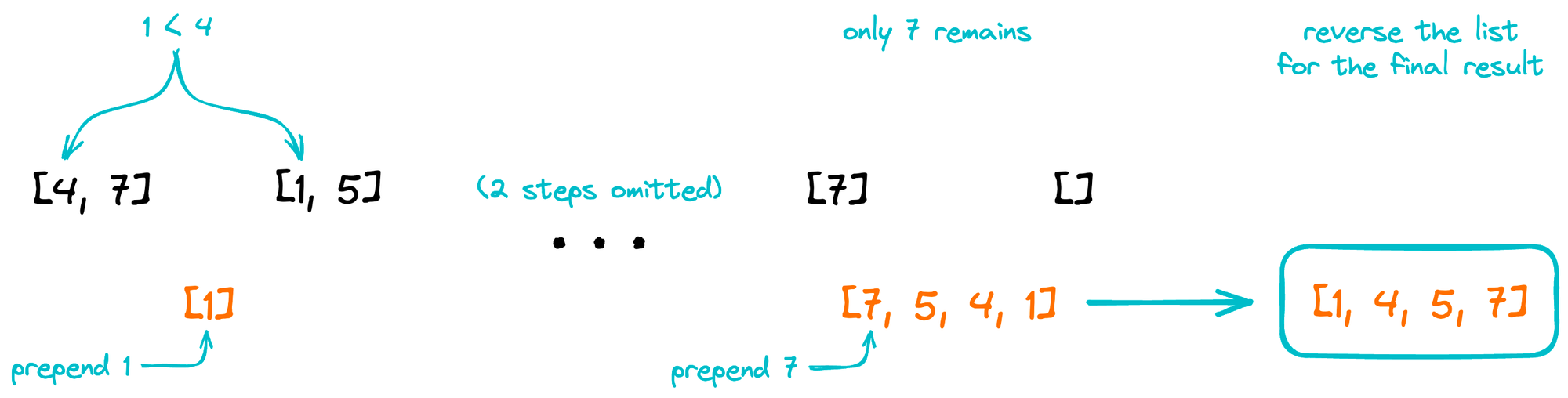
Merging a pair of longer lists is a similar process:

The code for merge_sorted isn't that complex, but some care must be taken to handle different situations. Here's the code:

@spec merge_sorted(list(), list()) :: list()
def merge_sorted(left, right) do
  do_merge_sorted(left, right, [])
end

@spec do_merge_sorted(list(), list(), list()) :: list()
defp do_merge_sorted([], [], merged) do
  Enum.reverse(merged)
end

defp do_merge_sorted([], [h | t], merged) do
  do_merge_sorted([], t, [h | merged])
end

defp do_merge_sorted([h | t], [], merged) do
  do_merge_sorted(t, [], [h | merged])
end

defp do_merge_sorted([hl | tl] = left, [hr | tr] = right, merged) do
  if hl < hr do
    do_merge_sorted(tl, right, [hl | merged])
  else
    do_merge_sorted(left, tr, [hr | merged])
  end
end

I introduce the private function do_merge_sorted to do the heavy lifting with recursion and the accumulation of the output. The first three clauses of do_merge_sorted handle the cases where one or both input lists are empty. The final clause handles the more general case of non-empty lists.

And that's it! I hope this was instructive and enjoyable. For the complete code, see this gist.